Second degré


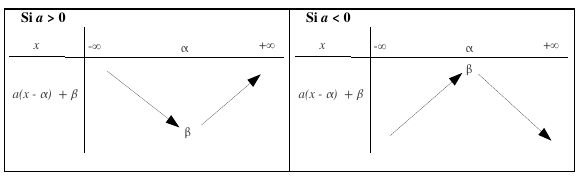
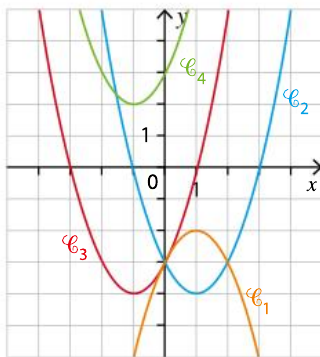
Fonction du second degré

On appelle fonction du second degré toute fonction f définie sur \mathbb{R} de la forme :
f (x) = ax^2 + bx + c
où a, b et c sont dans \mathbb{R} et a \neq 0.

Remarques

  • Un fonction du second degré aussi appelé polynôme du second degré.
  • On utilise plutôt P(x) que f(x).
  • Attention que la définition porte sur la forme.

Exercice 1

Déterminer si les fonctions ci-dessous sont des fonctions du second degrès ou non.
  1. f(x) = 3x^2 - 5x +1
  2. i(x) = \dfrac{9}{x^2} + x - 3
  3. g(x) = x^2 - \frac{5}{3}
  4. h(x) = 3x - x^2 +2 + 3x^2
  5. m(x) = x^3+2x-1
  6. p(x) = (3x-2)(4x+1)
  7. m(x) = 2(x-1)^2 -2x^2 + 3x + 5

Exercice

Déterminer les coefficients a,~ b et c de l'expression réduite des fonctions du second degré suivantes :

  1. 3x^2 - 5x +1
  2. x^2 - 5
  3. 3x - x^2 +2
  4. \dfrac{9x^2 + x -6}{3}
  5. (3x-2)\times(4x+1)
  6. 2(x-1)^2+3

Définition

La représentation graphique d'un polynôme du second degré s'appelle une parabole.
  • Si a \gt 0, elle ouverte vers le haut.
  • Si a \lt 0, elle ouverte vers le bas.

Forme canonique

Soit P(x)=ax^2+bx+c, un polynôme du second degré, avec a,~b,~c~ dans \mathbb{R} ,\ a \not= 0.
Alors il existe \alpha\in\mathbb{R} et \beta\in\mathbb{R} tel que P(x) s'écrit :
P(x)=a(x-\alpha)^2+\beta

C'est la forme canonique du fonction, avec \alpha=-\dfrac{b}{2a} et \beta = c - \dfrac{b^2}{4a} .

Démonstration

Vérifions :
a(x - \alpha )^2 + \beta = a \left(x - \dfrac{-b}{2a} \right)^2 + c - \dfrac{b^2}{4a} a(x - \alpha )^2 + \beta = a \left(x + \dfrac{b}{2a} \right)^2 + c - \dfrac{b^2}{4a} a(x - \alpha )^2 + \beta = a \left(x^2 + \dfrac{b}{a}x + \dfrac{b^2}{4a^2} \right) + c - \dfrac{b^2}{4a} a(x - \alpha )^2 + \beta = ax^2 + bx + \dfrac{b^2}{4a} + c - \dfrac{b^2}{4a} a(x - \alpha )^2 + \beta = ax^2 + bx + \cancel{\dfrac{b^2}{4a}} + c - \cancel{\dfrac{b^2}{4a}} a(x - \alpha ) 2 + \beta = ax^2 + bx +c

Exercice 3

Déterminer la forme canonique des fonctions du second degré suivante :
  1. f(x) = 3x^2 + 3x + 7
  2. g(x) = 5x^2 -2 x - 10
  3. h(x) = -\dfrac{2}{3}x^2 + 6x -3
  4. i(x)= 3x^2 + \sqrt{15}x + 9

Variations

Les variations du signe d'un fonction dépendent de a

Démonstration

Soit f la fonction fonction dont la forme canonique est
f(x) = a(x - \alpha)^2 + \beta

Cas a \gt 0.
Soit 2 réels u et v de l'intervalle ]-\infty ; \alpha] tels que u \lt v.
Le but de la démonstration est prouver que sur cet intervalle avec a \lt 0 la fonction f est décroissante.
C'est à dire de démontrer que si :
u \textcolor{red}{\lt} v
f(u) \textcolor{red}{\gt} f(v)

Cas où a>0 et v \in ]-\infty~;~\alpha]

u \lt v
u - \alpha \lt v - \alpha
u et v appartiennent à l'intervalle ]-\infty ; \alpha]
donc u - \alpha \lt 0 et v - \alpha \lt 0.
Or la fonction x^2 est décroissante sur l'intervalle ]- \infty~;~0]
(u - \alpha ) ^2 \textcolor{red}{\gt} (v - \alpha)^2
(u - \alpha ) ^2 + \beta \gt (v - \alpha)^2 + \beta
\textcolor{red}{f(u) \gt f(v)}
Dresser le tableau de variation des fonctions du second degré suivantes :


  1. f(x)= (x-1)^2 + 4
  2. g(x)= -2(x+3)^2 - 7
  3. h(x) = 3x^2 - x + 7
  4. i(x) = 5x + x^2 -3
Sans calculatrice, associer fonction ci-dessous à la courbe qui lui correspond.
  • f(x) = x^2-2x -3
  • g(x) = x^2 + 2x -3
  • h(x) = x^2+2x + 3
  • f(x) = -x^2 + 2x - 3

Exercice 6 : Optimisation

Un constructeur automobile décide de commercialiser des voitures à bas coût : chaque voiture doit être vendue 6 milliers d’euros. Sa production q peut varier entre 0 et 100 milliers de voitures.
Suite à une étude réalisée, les coûts de production (en million d’euros) sont donnés par la formule suivante :
C (q) = 0,05q^2 + q + 80 (q exprimé en millier d’unités).

  1. Exprimer, en fonction de q, la recette notée R (q) , en million d’euros.
  2. En déduire, en fonction de q, la fonction polynôme du second degré B qui donne le bénéfice réalisé par l’entreprise.
  3. Quel est le nombre d’automobiles à produire pour obtenir un bénéfice maximal ?



Al-Khwarizmi

Muhammad Al-Khwarizmi est un mathématicien, géographe et astronome perse du IX siècle, originaire de l’actuel Ouzbékistan. Le plus célèbre de ses écrits, Kitâb al-jabr wa al-muqâbala, que l’on peut traduire par « le livre du rajout et de l’équilibre », fut traduit en latin au XII ème siècle, sous le titre Algebra.
Traitant de la résolution des équa- tions du second degré, il est considéré comme le premier manuel d’algèbre (le terme vient d’al-jabr).

Activité

Au début du IXe siècle, le calife Al-Mamum réunit à Bagdad les principaux scientifiques perses de l’époque. À sa demande, Al-Khwarizmi (780-850) a rédigé un traité sur la résolution de problèmes de la vie courante.
Il y introduit un nouvel outil, les équations, dont il propose des résolutions algorithmiques. Dans son traité, Al-Khwarizmi propose de résoudre une équation énoncée ainsi :
Un mal et dix de ses racines égalent trente-neuf dirhams.

Activité

Un mal et dix de ses racines égalent trente-neuf dirhams.
Traduit en langage actuel, cet énoncé devient :
« Trouver un nombre tel que son carré ajouté à dix fois lui-même vaille 39. »

  1. Si x désigne la « racine » et x^2 le « mal », quelle est l’équation proposée par Al-Khwarizmi ?

Activité

  1. Pour déterminer une solution, Al-Khwarizmi énonce le procédé ci-dessous.
    Prends la moitié du nombre de racines, cela fera 5.
    Tu la multiplies par lui-même, cela fera 25.
    Additionne-les à 39, cela fera 64.
    Tu prends la racine qui est huit, dont tu retranches la moitié des racines qui est 5.
    Il restera 3 qui est la racine du carré que tu cherches.
    Vérifier que le nombre réel qu'il obtient est bien solution de l'équation.

Activité

  1. Pour justifier ce procédé, Al-Khwarizmi s'appuie sur une figure géométrique.
    Il cherche à déterminer le côte x d'un carré ABCD tel que si, on lui juxtapose deux rectangle BEFC et DCHI de côtés x et 5, on obtienne un polygone AEFCHI d'aire égale à 39.
    1. En exprimant de deux manière l'aire du polygone AEFCHI en fonction de x, vérifie que pour tout nombre réel x positif, x^2 +10x = (x+5)^2 -25
    2. Montrer que l'équation d'Al-Khwarizmi est équivalente à (x+5)^2 -64 = 0.
    3. Résoudre cette équation.
  2. De la même manière, résoudre x^2+8x = 20.

Racines d'un polynôme de second degré.

Discriminant

On appelle discriminant, noté \Delta, le nombre b^2 - 4ac.

Propriété

On considère l'équation (E) :
ax^2 + bx + c = 0
Si \Delta \gt 0
Alors (E) a deux solutions :
x_1 = \dfrac{-b - \sqrt{\Delta}}{2a}
x_2 = \dfrac{-b + \sqrt{\Delta}}{2a}

Si \Delta = 0
Alors (E) a une solution :
x_1 = \dfrac{-b}{2a}

Si \Delta \lt 0
Alors (E) n'a pas de solution :

Exercice 7

Pour chacune des équations ci-dessous déterminer le nombre de solutions.
  1. x^3 - 4x - 12 = 0
  2. -2x^2 + 4x - 1 = 0
  3. x^2 - x + 1 = 0

Exercice 8

Résoudre dans \mathbb{R} les équations suivantes :
  1. -2x^2 + x -1 = 0
  2. 2x^2 -2x -1 = 0
  3. 5x^2 -2x +1 = 0
  4. x(2x -1) = 1
  5. x^2 = -5x -1
  6. -x +3x^2 -1 = 0
  7. x(8-x) + 1 = 0
  8. 2x^2 + 6x +\dfrac{9}{2} = 0
  9. x^2 + 2\sqr{3}x + 3 = 0
  10. -3x^2 + x = -\dfrac{1}{4}
  11. 2x(5+2x) = 9 - 2x

Exercice 22 p.66

Exercice 28 p.68

Forme factorisée

Soit P(x) un polynôme du second degré tel que P(x) =ax^2 + bx + c

Cas n°1 : \Delta \gt 0
La forme factorisée de P(x)= a(x -x_1)(x - x_2) ou x_1 et x_2 sont les racines de P(x)
Cas n°2 : \Delta = 0
La forme factorisée de P(x)= a(x -x_1)^2 ou x_1 est la racine de P(x).
Cas n°3 : \Delta \lt 0
P(x) n'a pas de forme factorisée.

Etude du signe d'un trinôme

Cas ou \Delta > 0

Cas ou \Delta = 0

Cas ou \Delta < 0

Application

Pour chacun des polynôme du second degrés ci-dessous. Dresser son tableau de signe.
  • f(x) = 2x^2 - 2x - 12
  • g(x) = -5x^2 + 40x - 80
  • h(x) = -x^2 + 3x - 13
  • i(x) = 4(x - 15)^2 + 40

Somme et produit des racines d'un trinome

Grenouille

Les bonds des animaux sauteurs ont des trajectoires paraboliques.

Considérons le bond d’une grenouille. Lorsqu’elle saute sur un sol plat, la longueur de son saut est de 2,7 mètres et la hauteur maximale au-dessus du sol est de 0,9 mètres.
Ce bond lui permettra-t-il de passer au dessus d’un bac à fleurs de 65 centimètres de haut de 1,6 mètres de large ?

Propriété

Soit le polynôme du second degré P(x)= ax^2+bx +c où a \neq 0 et a,~b,~c sont des réels.
Si P admet deux racines distinctes x_1 et x_2 alors
  • Somme des racines de P : x_1 + x_2 = - \dfrac{b}{a}
  • Produit des racines de P : x_1 \times x_2 = \dfrac{c}{a}